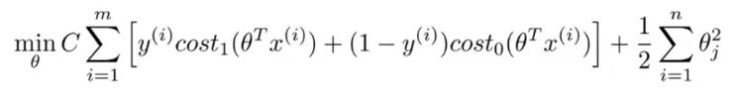Support Vector Machine – Linear Decision Boundary

• Decision Boundary ( Ranh giới quyết định)
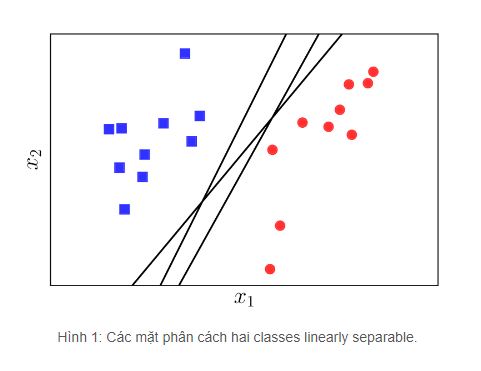
  • Trong bài toán phân loại nhị phân, chúng ta cần xác định 1 đường chia cắt 2 class khác nhau thành 2 vùng riêng biệt để từ đó với mỗi đầu vào mới ta sẽ dự đoán kết quả của nó thuộc class nào. Đó là ranh giới quyết định.
  • Tuy nhiên khi training một thuật toán hồi quy logistic thì có thể ta nhận được nhiều ranh giới khác nhau ví dụ như hình dưới: ( ảnh nguồn: machinecb.com)
    • 
    • Chúng ta có 3 đường kẻ đen đều là Decision Boundary.
  • Vậy đường kẻ nào là tốt nhất.
    • Người ta định nghĩa một đường kẻ tốt là đường kẻ mà có tổng khoảng cách đến điểm gần nhất của 2 class bằng nhau và là lớn nhất.
  • Nhìn vào ảnh sau:
    • 
    • Hình trên biểu diễn khoảng cách từ đường ranh giới đến điểm gần nhất của class đỏ và class xanh. Rõ ràng ở đây ta thấy khoảng cách của chúng đến đường ranh giới không đều. Vì vậy đây không phải đường ranh giới tốt nhất
  • Ta lại có ảnh:
    • 
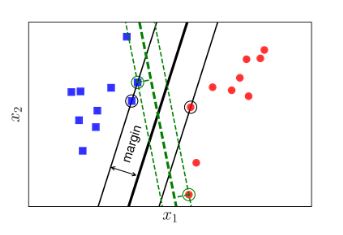
    • Ở ta có 2 đường ranh giới là đường màu đen nét liền to và đường màu xanh lục nét đứt.
    • Nhìn vào đường màu xanh lục nét đứt ta thấy khoảng cách của nó tới điểm gần nhất của 2 class là bằng nhau. Tuy nhiên nhìn vào đường màu đen nét liền ta cũng thấy khoảng cách từ nó đến 2 điểm gần nhất của 2 class cũng bằng nhau. Vậy đường nào tốt hơn.
    • Đáp án là đường nào có tổng khoảng cách lớn hơn thì đường đó tốt hơn. Và đó là đường đen nét liền.
    • Khoảng cách từ đường đen đến điểm gần nhất ta gọi là margin
  • Việc có margin rộng hơn và đều hơn đem lại sự phân chia chuẩn xác hơn đối với 2 class và nó cũng sẽ khiến cho thuật toán của chúng ta ít lỗi hơn với dữ liệu đầu vào mới
  • Bài toán tối ưu trong Support Vecter Machine chính là bài toán tìm được đường ranh giới sao cho margin đều và lớn nhất.
• Support Vecter Machine trong phân loại nhị phân
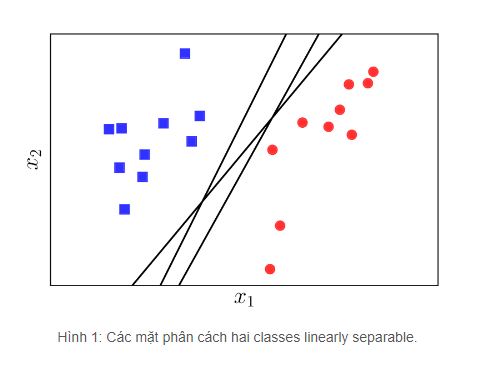
  • Ta có Cost Function của hồi quy logistic như sau:
    • 
  • Ta gọi phép tính log với hx là một phép tính cost của theta^T * X. Ví dụ như sau:
    • 
  • Sau đó ta đặt C = 1/lambda. Cuối cùng nhân cả CostFunction J của hồi quy logistic với C và m. Rút gọn ta được Cost Function J(svm) mới như sau:
    • 
  • Khi chúng ta tìm được min của J(svm) thì để biểu thức xích-ma đạt min thì ta nên chọn giá trị C lớn. Khi đó biểu thức xích-ma sẽ được giá trị cực nhỏ và đồng thời giá trị của theta^T * X cũng clear hơn.
    • Với nhãn y = 1 thì theta^T * X >= 1
    • Ngược lại y = 0 thì theta^T <= -1
    • Xem ảnh sau:
    • 
  • Cuối cùng khi J(svm) đạt min và C của chúng ta lớn. Kéo theo theta^T * X có giá trị nằm ngoài khoảng (-1;1) thì biểu thức 1/2 tổng của bình phương các theta cũng đạt min.
    • Ta biết norm 1 của vecter theta sẽ bằng căn bậc 2 của tổng bình phương các phần tử trong vecter theta.
    • vậy rõ ràng biểu thức phía sau sẽ biến đổi thành 1/2*(||theta||^2)
    • ngoài ra biểu thức theta^T * X = khoảng cách từ X tới theta nhân với norm 1 của theta. Ta gọi khoảng cách đó là P.
    • Vậy theta^T * X = P . ||theta||.
    • Mà khi J(svm) đạt min thì biểu thức 1/2 tổng của bình phương các theta cũng đạt min. Hay chính xác hơn là norm 1 của theta cũng đạt min.
    • Chính vì vậy để P . ||theta|| >= 1 hoặc P . ||theta|| <= -1 khi ||theta|| rất nhỏ thì P dương (khi x có nhãn y = 1) sẽ phải rất lớn và P âm ( khi x có nhãn y = 0) cũng vậy. Chính vì vậy khoảng cách P đến các điểm của từng class cũng đạt giá trị lớn nhất.
  • Đó là chứng minh vì sao khi ta minimize cost function J(svm) thì lại có thể tìm được bộ theta giúp ta xây dựng được đường ranh giới tối ưu nhất
  • Lưu ý khi chọn tham số C. Vì C = 1/lambda. Nếu ta chọn C quá lớn đồng nghĩa với việc lambda quá nhỏ. Rất có thể sẽ dẫn tới việc hàm giả thuyết bị high variance.